泸定中学第一学期初中三年级数学期中考试题
（考试时间100分钟，满分150分）
一．选择题（本大题共6题，每题4分，满分24分）
【下列各题的四个选项中，有且只有一个是正确的，选择正确项的代号并填涂在答卷纸的相应地方上】
1．若
，则下列比率式正确的是…………………………………………………（ ）
（A）
； （B）
； （C）
； （D）
．
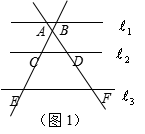
2． 如图1，已知
，直线AF交直线
于点A、D、F，直线BE交直线于点B、C、E下列比率式中正确的是………………………………………（ ）
（A）
； （B）
； （C）
； （D）
．
3．如图2，△ABC中，DE//BC交AB于点D，交AC于点E，假如
，那样下列等式成立的是 …………………………………………………………………（ ）
（A）
； （B）；
（C）
； （D）
．
4．假如非零向量，那样下列结论正确的是 ………………………………（ ）
（A）
； （B）
； （C）
； （D）
．
5． 如图3，在Rt△ABC中，∠ACB=
，CD⊥AB于D，下列式子正确的是（ ）
（A）
； （B）
； （C）
； （D）
．
6．下列各组图形必一样的是……………………………………………………………（ ）
（A）任意两个等腰三角形；（B）有两边对应成比率，且有一个角对应相等的两三角形；
（C）两边为4和5的直角三角形与两边为8和10的直角三角形；
（D）两边及其中一边上的中线对应成比率的两三角形．
二．填空题（本大题共12题，每题4分，满分48分）
7．线段4和9的比率中项是__________．
8．在1∶10000000的地图上，量得两个城市间的距离是6cm，那样这两城市的实质距离
是__________千米．
9．点P为线段AB的黄金分割点（PA＞PB），则关于PA、PB、AB的比率式是______________________________．
10．等腰直角三角形斜边上的高与直角边之比为__________．
11．在△ABC中，若中线AD和中线CE相交于G，则
__________．
12．如图4，在边长相同的小正方形网格中，点
都在这类小
正方形的顶点上，
相交于点
，则
=__________．（图4）
13．已知两个相似三角形的相似比是9∶5，那样这两个三角形的周长比是____________________.
14．化简：
=__________．
15．已知
，假如
，那样__________．
16．如图5，矩形DEFG内接于△ABC，点D、E落在边BC上，BC=6cm，DE=3cm，EF=2cm，则BC边上的高的长是__________cm．
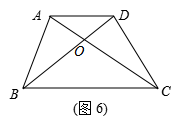
17．如图6，梯形ABCD中，AD//BC，对角线AC、DB交于点O，假如S△AOD∶S△ABD=2∶5，那样S△AOD∶S△BOC=__________．
18．如图6，在Rt△ABC中，∠C=90°，AC=3，AB=5，点D、E分别是边BC、AC上的点，且∠EDC=∠A，将△ABC沿DE翻折，若点C恰好落在边AB上，则DE的长为____________________.
三．解答卷（本大题共7题，满分78分）
19．（本题满分10分）
计算:
20.（本题满分10分）
如图，在△ABC中，BD平分∠ABC，点E在AB边上，DE∥CB，若AE=2，BC=4，求线段DE的长．
21、（本题第（1）题5分，第（2）题5分，满分10分）
如图,四边形ABCD是平行四边形，E是BA延长线上一点，CE交AD于点F，EA:AB=3:2,
求：△EAF与△EBC的周长比 若S△EAF=18cm2，求S△DCF
22．（本题第（1）题5分，第（2）题5分，满分10分）
冬至是一年中太阳光照射最少的日子，假如此时楼房最低层能采到阳光，一年四季整座楼均能遭到阳光的照射，所以冬至是选房买房时确定阳光照射的最好机会。某居民小区有一朝哪个方向为正南方向的居民楼。该居民楼的一楼是高6米的小区超市，超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海区域冬至正午的阳光与水平线夹角为29°.
中午时，超市以上的居民住房采光是不是有影响，为何？
若要使得超市楼上采光不受影响，两楼应至少相距多少米？（结果保留整数）
23．（本题第（1）题6分，第（6）题6分，满分12分）
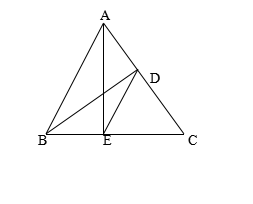如图，在△ABC中，AE、BD分别是BC、AC边上的高，连结DE．
（1）求证：△AEC∽△BDC；
（2）假如＝4︰5，求cosplayC的值．
24（本题第（1）题4分，第（2）题8分，满分12分）
已知：如图，
中为上一点，，，
，
，点
为垂足，联结
。
求的度数；
求证：
25.（本题共3小题，第小题6分，第小题5分、小题每小题3分，满分14分）如图，等腰中，，
，为腰上的中点，是底边 上一动点（与
、
不重合），作射线DF交边AB于F，且
，
设
，
，求关于
的函数分析式，并写出的取值范围；
若
，求；
是不是存在一点，使为等腰三角形，若存在，请求出的长，若没有，请说明理由。
2017学年度第一学期初三数学期中考试试题答案
1、C C D B D C
2、7. 6； 8. 
； 9.400 ； 10. 
；
11. 4 ； 12. 
； 13. 、、、； 14. ； 15. 
；
16. ； 17. ； 18. 
。
19. 解：（1）D是AB的中点，且AB=12，
AD=， …………………………1分
在与
中，
∽ …………………………2分
…………………………2分
=72…………………………1分
AC=；…………………………1分
（2）要作图；； 。…………………………3分
20. 解：（1）将点B（-1,0）、C（2,3）代入，
得：，………2分 解得： ……………4分
此抛物线的表达式为. ……………1分
（2）在中，当时，
，…………1分
若点（-2，-5）平移后的对应点为（-2，-1），则需将抛物线向上平移4个单位。
（办法不唯一，其他办法酌情给分） ………………2分
21解：DE//BC,
, ……………2分
DE=6, BC=9；……………2分
（2） DE//BC, ……………1分
，……………1分
∽……………2分
FA=6，FE=4，
DF=9。……………2分
22. 解：与一样的三角形有：AGD、FGH、CEH；…………3分
（2）选证：与相似。 ……………1分
、均为等边三角形，
，
……………1分
，即：
……………2分
在与中，
……………2分
∽ ……………1分
23. 证明：四边形ABCD是正方形
AB//CD，即BN//CD，且AB=CD …………………………2分
…………………………2分
…………………………1分
AB=CD
…………………………1分
（2）解：设DM=
MN=1, PN=3, …………………………1分
AB//CD
AN//CD且BN//CD…………………………1分
…………………………1分
且 
…………………………1分
=1 …………………………1分
解得：
DM=2 …………………………1分
24.（1）由题意原抛物线经过点A（4,0），B（0,8） ……………1分
代入得：
解得：
………………………2分
原抛物线表达式： ………………………1分
平移后的抛物线表达式： ………………………1分
点C（1,3） ………………………1分
（2）设直线AB的分析式为：
过点A（4,0）和点B（0,2）
………………………1分
抛物线的对称轴与线段AB交于点P
P（） ………………………1分
由题意的
与
相似有两种可能：
1°，得CQ=4；点Q（1，-1） ………………………2分
2°，得CQ=； 点Q（1，
）………………………2分
25. 证明: AB∥DC，∠ABD=∠BDC ………………………1分
∠ABD =∠C，∠BDC =∠C ……………………………1分
∠BPD =∠BPE+∠EPD
∠BPD =∠PBC+∠C
又∠BPE =∠C
∠PBC =∠EPD ……………………………………1分
△BCP∽△PDE …………………………………………1分
△BCP∽△PDE
, ……………………………………………………1分
CP= x , BE=y，BD=BC=4,CD=6
DP= 6 - x , DE= 4 – y
, …………………………………………………1分
（0
能。 ………………………1分
若BP=PE，则△BCP≌△PDE，
PD=BC=4, x=2 ……………………………………………2分
若BE=PE，则∠BPE=∠PBE=∠C=∠CDB，
△BEP∽△CBD，PE：PB=BC：CD=2：3
又PD：BC=PE：PB
即（6-x）：4=2：3，
x=
……………………………………………………2分
若BP=BE，则∠BPE=∠PEB>∠CDB，矛盾. ……………………1分
当x=2或时，△BPE为等腰三角形.
